Les propriétés fascinantes de l’identité remarquable : degré 3 décryptées

Les propriétés fascinantes de l’identité remarquable : degré 3 décryptées
Les identités remarquables jouent un rôle crucial dans le domaine des mathématiques, notamment lors du développement et de la factorisation d’expressions algébriques. Les identités remarquables de degré 3, bien que souvent négligées, possèdent des propriétés fascinantes qui méritent d’être explorées. Dans cet article, nous plongerons au cœur de ces identités, tout en découvrant leur utilité et leur application dans divers contextes mathématiques.
Les identités remarquables de degré 3 : définitions et fondements
Les identités remarquables de degré 3 sont des égalités algébriques qui facilitent la manipulation des polynômes. Par exemple, on trouve deux identités fondamentales :
- (a – b)³ = a³ – 3a²b + 3ab² – b³
- (a + b)³ = a³ + 3a²b + 3ab² + b³
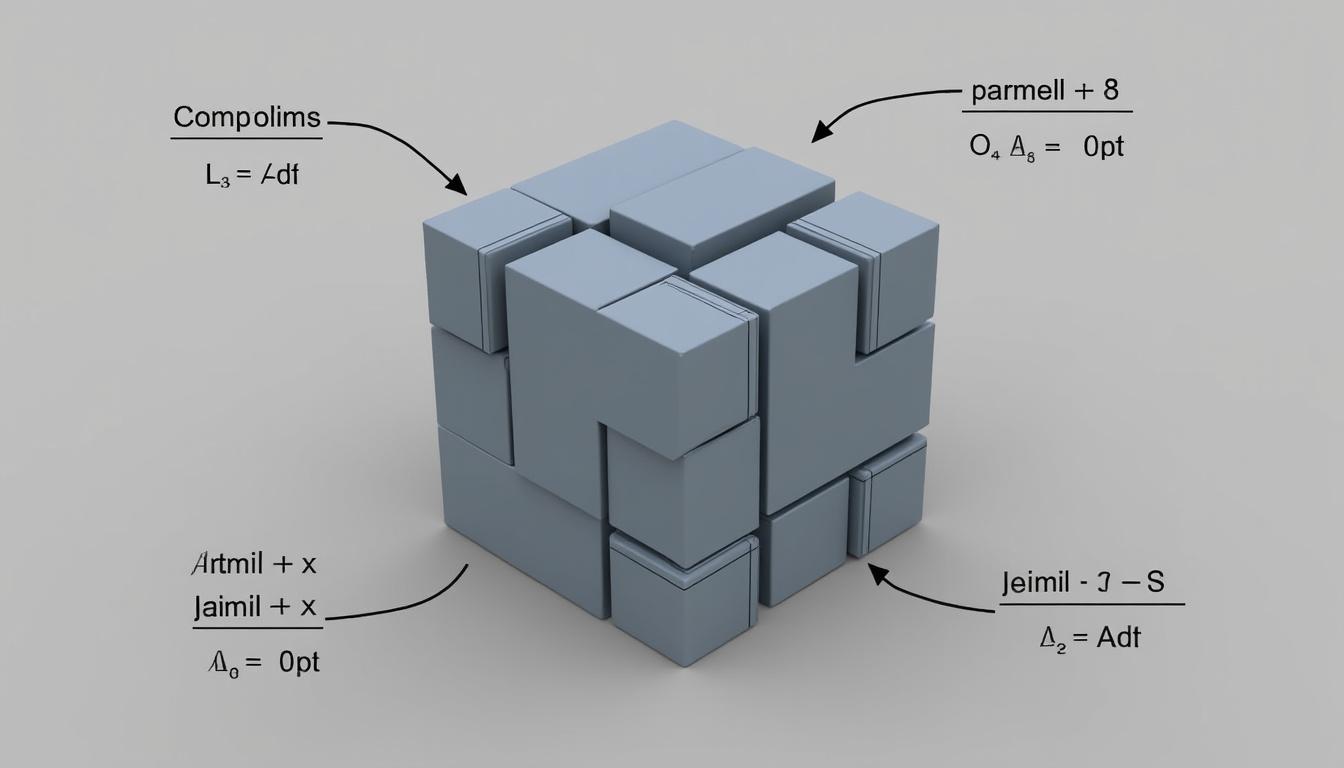
Ces équations peuvent paraître abstraites, mais elles prennent sens lorsque l’on les considère à travers des applications concrètes. Pour comprendre ces identités, envisageons une représentation géométrique. Imaginons un cube dont les côtés mesurent (a + b). En développant le volume de ce cube, nous pouvons le faire de deux manières : en le considérant comme le cube de (a + b) ou en soustrayant un cube de côté b du volume total. Ceci mène à des résultats identiques et illustre la beauté intrinsèque des identités remarquables.
Au-delà de la théorie, ces identités sont d’une grande utilité. Non seulement elles nous aident à résoudre des équations, mais elles ouvrent aussi des portes à la compréhension des polynômes et de leurs relations.
L’application des identités de degré 3 dans les calculs
L’utilisation des identités remarquables de degré 3 s’étend à divers domaines des mathématiques. Par exemple, elles sont essentielles lors de la facturation de polynômes ou dans le cadre d’équations plus complexes. Prenons, par exemple, l’application de (a – b)³ dans un problème d’optimisation. Imaginons une situation dans laquelle une entreprise souhaite réduire ses coûts de production. L’utilisation de cette identité permettra de modéliser des coûts via des équations polynomiales, rendant ainsi possibles des analyses précises.
Considerons une équation de coût C(a, b) = (a – b)³. En appliquant cette identité, nous obtenons :
| a | b | Coût C(a, b) |
|---|---|---|
| 10 | 2 | 512 |
| 7 | 4 | 27 |
| 5 | 3 | 8 |
Ce tableau illustre comment, en utilisant (a – b)³, nous pouvons rapidement évaluer le coût en fonction des variations de a et b. La simplicité de l’identité, jointe à sa puissance, en fait un outil précieux pour les étudiants et les professionnels du secteur.
Conversion et transformation d’expressions algébriques
Les identités remarquables de degré 3 ne se contentent pas de développer ou de factoriser des polynômes ; elles facilitent également la transformation d’expressions algébriques complexes. Séparer un terme dont le degré est élevé permet de simplifier les calculs. En d’autres termes, ces identités agissent telles des « raccourcis » mathématiques.
Un exemple fréquent dans les exercices d’algèbre consiste à utiliser ces identités pour passer d’une forme à une autre, rendant ainsi les calculs plus faciles. Supposons que l’on ait l’expression a³ + b³, qui peut être factorisée grâce à l’identité suivante :
- a³ + b³ = (a + b)(a² – ab + b²)
Ici encore, la visualisation géométrique peut aider à comprendre cette transformation. En considérant deux cubes dont les côtés mesurent a et b, on peut comprendre intuitivement comment leurs volumes interagissent. Cette approche offre une dimension supplémentaire à notre compréhension des polynômes.
Exercices pratiques pour maîtriser les identités remarquables
Pour bien assimiler les identités remarquables de degré 3, une série d’exercices peut être mise en place. Voici quelques exemples d’applications pratiques :
- Développez l’expression (x + 2)³.
- Factorisez l’expression x³ – 3x²y + 3xy² – y³.
- Calculez la valeur de (5 – 3)³ et de (5 + 3)³.
Chaque exercice offre une occasion de mettre en pratique les identités de manière concrète. Ces défis permettent aux étudiants et aux praticiens de développer une certaine aisance dans la manipulation des polynômes.
Le lien entre identités remarquables et développement personnel
De manière intéressante, on pourrait voir les identités remarquables non seulement comme des outils mathématiques, mais aussi comme une métaphore de notre propre développement personnel. En effet, tout comme ces identités nous aident à travailler avec des termes plus complexes, elles soulignent l’importance de reconnaître et de développer nos propres talents et capacités.
Chaque individu possède son propre « cube » – une combinaison unique de compétences et de passions. Savoir rassembler ces éléments est essentiel pour former une identité forte et authentique. Par exemple, quelqu’un ayant des compétences artistiques et analytiques peut créer un mélange unique, formant ainsi une « signature authentique ».
Cet axe d’analyse pourrait mener à une réflexion sur la valeur de notre unicité dans un monde où la standardisation est souvent la norme. La valorisation de l’Essence Distinctive de chaque personne peut faire la différence dans les contextes professionnels et personnels.
Comment les identités influencent la créativité et l’innovation
Étant donné que les identités remarquables de degré 3 fournissent des stratégies pratiques pour résoudre des problèmes, elles incitent également à l’innovation. Les mathématiques et la créativité sont souvent perçues comme opposées, mais, en réalité, elles se nourrissent l’une de l’autre.
Prendre un exemple concret : la réputation de certaines marques de technologie, comme Apple ou Google, repose sur leur capacité à innover. Ces entreprises utilisent des outils mathématiques complexes, y compris des identités semblables aux identités remarquables, pour optimiser leurs algorithmes et créer des expériences utilisateur exceptionnelles.
En définitive, comprendre les identités remarquables peut enrichir la manière dont on aborde des défis, qu’il s’agisse de créer un nouveau produit ou de résoudre un problème à l’école. Cela montre donc l’importance d’une éducation mathématique robuste qui favorise les innovateurs de demain.
Comparaison entre identités de degrés différents
Les identités remarquables ne s’arrêtent pas à celles de degré 3. Il existe également des identités de degré 2 qui sont souvent utilisées, notamment :
- (a + b)² = a² + 2ab + b²
- (a – b)² = a² – 2ab + b²
Il est intéressant de comparer ces deux groupes d’identités. Les identités du degré 2 sont souvent plus simples et enseignées dès le début de l’apprentissage des mathématiques. En revanche, celles du degré 3, bien que plus complexes, offrent une profondeur supplémentaire lors de l’analyse de relations entre polynômes.
Une manière efficace de mieux saisir la différence consiste à établir un tableau de comparaison :
| Identité | Degré | Utilité principale |
|---|---|---|
| (a + b)² | 2 | Développement simple d’expressions |
| (a – b)² | 2 | Factorisation |
| (a + b)³ | 3 | Manipulations complexes et modélisations |
| (a – b)³ | 3 | Applications d’optimisation |
Ce tableau permet ainsi de voir non seulement une différence en termes de complexité, mais également comment chaque identité peut répondre à des besoins mathématiques spécifiques. C’est une réflexion essentielle pour quiconque désire approfondir ses connaissances en algèbre et dans les mathématiques en général.
Intégration des identités remarquables dans le quotidien
Il est fascinant de se rendre compte à quel point les identités remarquables de degré 3 peuvent s’intégrer dans des aspects très quotidiens de notre vie. Qu’il s’agisse de la planification budgétaire, de la conception de projets architecturaux ou même de la modélisation de performances sportives, la capacité à comprendre et à appliquer ces identités peut se révéler précieuse.
Les professionnels de divers secteurs, allant de l’ingénierie à la conception numérique, se voient souvent confrontés à des équations complexes. Il est ici pertinent de prendre un exemple d’application réelle, notamment dans le domaine de l’architecture :
- Calcul du volume d’un espace en utilisant le cubage de dimensions (a + b).
- Utilisation des identités dans des simulations pour optimiser l’espace disponible.
Ces applications démontrent comment la théorie mathématique peut se traduire par des impacts réels et tangibles dans un environnement de travail. En fin de compte, il s’agit là d’un précieux rappel que les mathématiques sont omniprésentes et que leur maîtrise peut s’avérer être un atout considérable.
Exploiter les identités remarquables dans l’éducation
D’un point de vue pédagogique, l’apprentissage des identités remarquables de degré 3 doit être encouragé dès le plus jeune âge. Les enseignants peuvent développer des outils engageants qui facilitent la compréhension de ces concepts. Cela pourrait inclure des jeux de société mathématiques, des applications interactives et des projets de groupe qui mettent à profit l’application des identités dans des contextes réels.
Des cas d’études montrent qu’une approche participative permet non seulement une meilleure compréhension mais également un renforcement de la confiance en soi chez les élèves. En parallèle, les professeurs pourraient intégrer des déplacements vers une approche basée sur l’intégration de la technologie pour rendre l’apprentissage encore plus engageant. Par exemple, une application permettant de visualiser les identités dans différents contextes géométriques pourrait renforcer la compréhension des étudiants.
Quelle est l’importance des identités remarquables de degré 3?
Ces identités facilitent le développement et la factorisation d’expressions algébriques, rendant les mathématiques plus accessibles.
Comment les identités sont-elles utilisées dans la vie quotidienne?
Elles sont utilisées dans des domaines variés tels que l’architecture, la gestion budgétaire et l’ingénierie.
Peut-on combiner les identités remarquables de degré 2 et 3?
Oui, les identités de degré 2 peuvent être intégrées dans des expressions de degré 3 pour les développer ou les factoriser.
Quelles ressources utiliser pour mieux comprendre ces identités?
Des livres d’exercices, des applications interactives et des tutoriels vidéo peuvent grandement aider.
Pourquoi est-il essentiel d’apprendre ces identités en mathématiques?
Cela permet de renforcer des compétences en algèbre et de préparer les étudiants aux mathématiques avancées.

